前言:学不求一次之多,而贵在周周复省。虽然时间很零碎,但也不强求自己能一天学多少,争取每天积累一点就行。
教程:李宏毅(Hung-yi Lee)的Linear Equations视频教程
ppt地址:http://speech.ee.ntu.edu.tw/~tlkagk/courses_LA18.html
视频地址:https://www.bilibili.com/video/av31780632/?p=5
由于想系统而深入学习机器学习的东西,所以将本科没有上过的线代学习一下,所以才有了这个读书笔记。
【向量】
什么是向量?
最简单的理解就是,一组数字的集合(a set of numbers)
按照行列分法,既可以分为行向量(Row vector)以及列向量(column vector)
向量的表示方法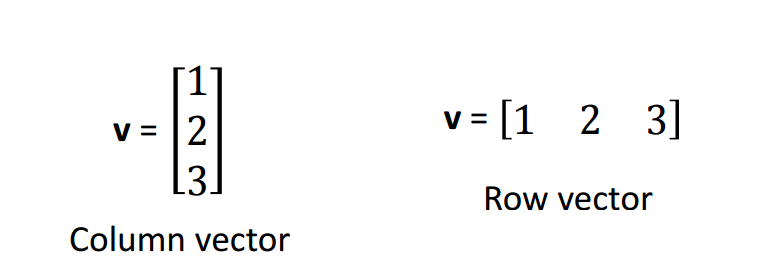
假定某向量为V,里面有n个元素,那么按照顺序,既可以将向量中的元素表示为V1,V2......Vn
当向量的元素少于4个的时候,既可以在平面上以几何的形式表示出来,既一维到三维的表示方法
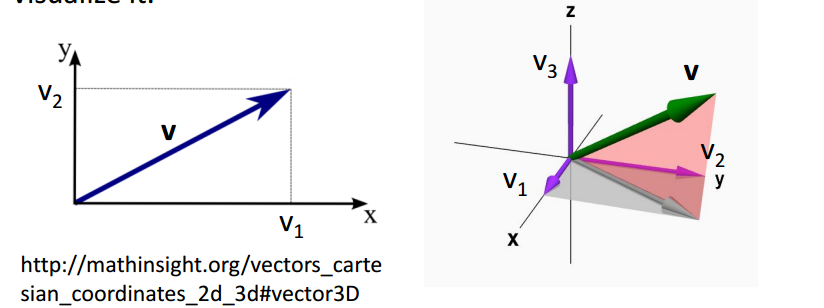
向量的运算
数乘运算(scalar multiplication)
类似于int类型数字的乘法,只不过是vector里面所有的components都与某个数相乘。
v = [1,2,3,4]
c =5
###此时v的数乘运算表示为cv,而其运算也是十分简单的
cv = [1*5,2*5,3*5,4*5]
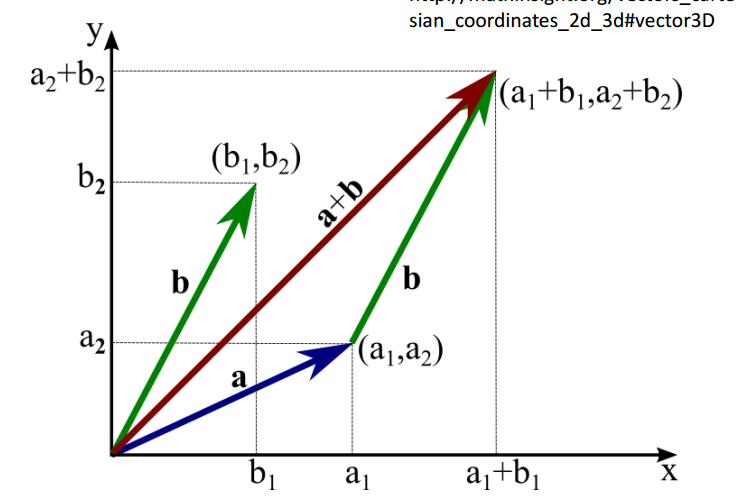
向量的加法(vector addition)
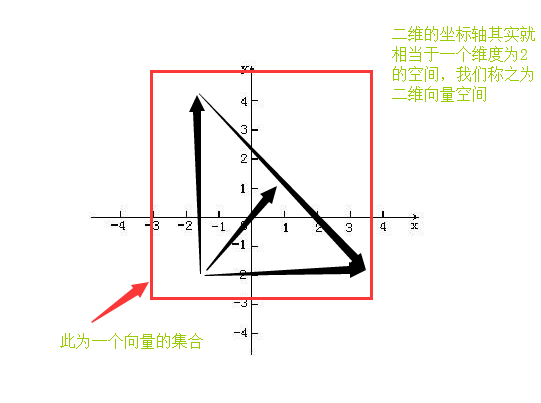
其实向量的加减是一个道理,即相应向量分量的加减,如何从字面理解这个意思,其实就是类似我们初高中物理里面的正交分解,力F1可以在二维轴上分解出F1x与F1y,力F2可以在二维轴上分解出F2x与F2y,然后在这个分解的坐标轴中,得到了一个很好的映射,从而将两者在该坐标轴上的关系理清,然后通过简单的加减,即可得到最后作用的结果。图例如下
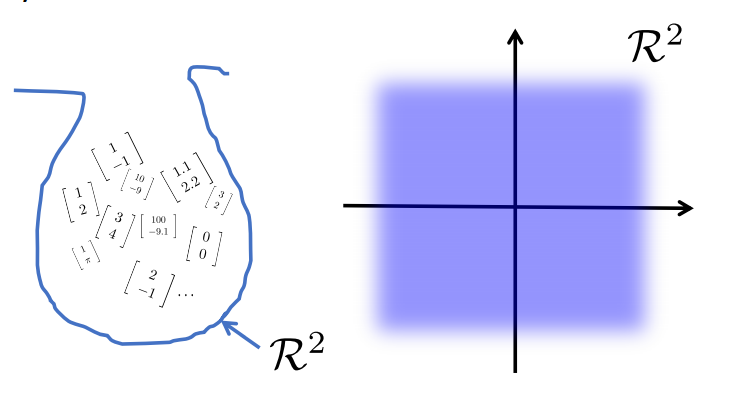
向量的集合(vector set)
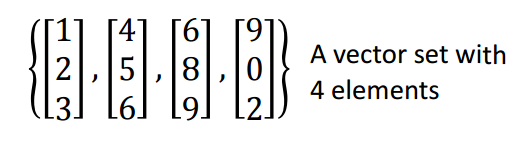
由不同的向量组合在一起,组成向量集合,如何理解,我们可以以只有两个元素的二维向量来简单的理解一下。
那么如何来表示这个集合呢,我们通常将这个集合以大写字母R表示,如果是2维的,表示为R2,如果是三维的,则为R3,以此类推
那么集合间是如何运算的呢?
首先,我们的运算必须是同一维度的,拿2维跟3维的进行运算,这有点超出想象。
那么这个集合的运算符合什么定律呢,看下图

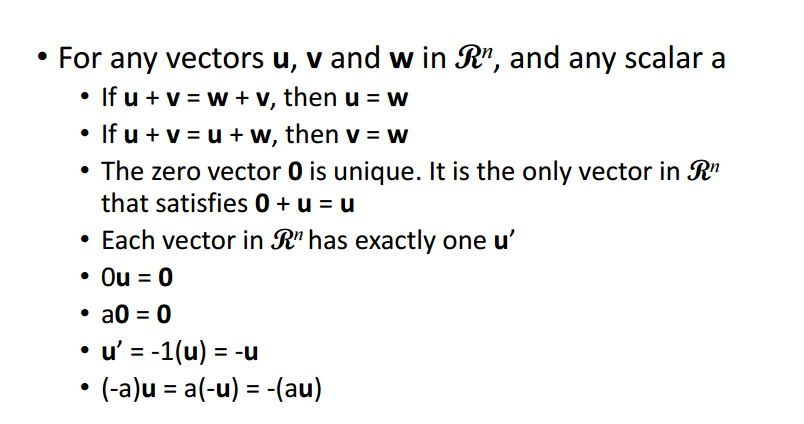
【矩阵】
什么是矩阵?
矩阵,就是一组向量的集合,也就是上面的vector set
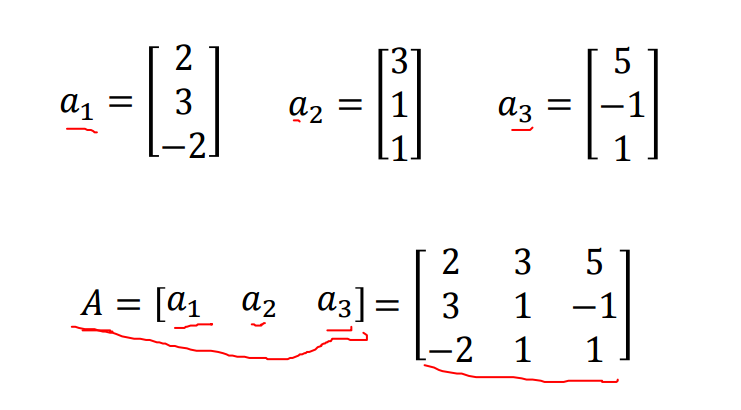
矩阵的表示
如果某矩阵有m行n列,那么我们就可以将其表示为Mmxn。记住一个原则

如何表示矩阵中的某个元素,其实也是先行后列的表示方法A矩阵的第三行,第四列的元素,表示为A34
矩阵的运算
首先是加减法,其实这很好理解,同一维度的才能进行加减,即两个矩阵具有相同的行列时才具备加减的条件
接着是数乘,其实就是向量数乘的延伸。
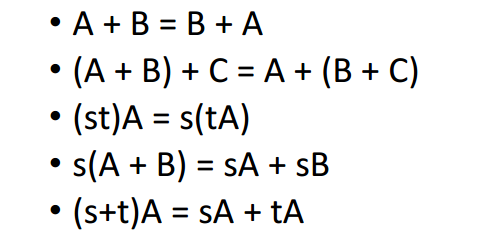
特殊矩阵,Zero matrix,顾名思义,都是0,可以表示为Omxn,个人认为,这就是一个多维空间中的一个奇点,有点奇妙
Identity matrix,除了对角线,其余都是零,这个也是很奇妙,在一个大于1的多维空间中,它是一条线(个人yy,不一定正确)
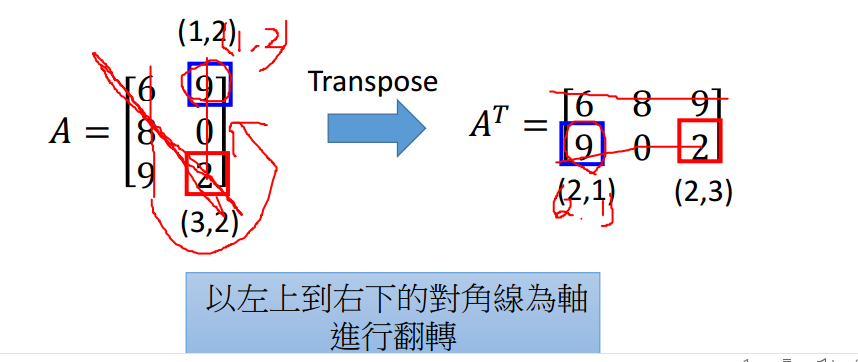
矩阵的转置(Transpose)
简而言之,就是行列互换(包括元素),个人觉得,这个类似于左右手的关系,即轴对称,在三维空间里,应该就是镜像的存在
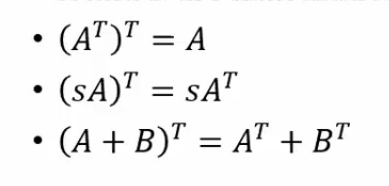
视频看了一个小时,然后对着ppt边敲字边截图,又过了一个小时,果然还是有点累